偶函数和奇函数的性质,偶函数和奇函数运算法则
高中数学中函数是必学知识点,也是必考知识点,所以学好函数是考高分的必备条件,其中奇函数和偶函数就属于函数中的重要函数,今天我们就来复习复习奇函数和偶函数的相关知识点,首先我们看看什么是奇函数,什么是偶函数?
奇函数:如果对于函数f(x)的定义域内任意一个x,都有f(-x)= - f(x),那么函数f(x)就叫做奇函数。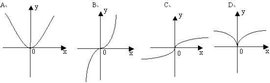
偶函数:如果对于函数f(x)的定义域内任意的一个x,都有f(x)=f(-x),那么函数f(x)就叫做偶函数。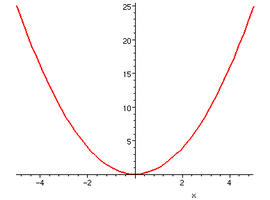

奇函数性质:
1、图象关于原点对称
2、满足f(-x) = - f(x)
3、关于原点对称的区间上单调性一致
4、如果奇函数在x=0上有定义,那么有f(0)=0
5、定义域关于原点对称(奇偶函数共有的)
偶函数性质:
1、图象关于y轴对称
2、满足f(-x) = f(x)
3、关于原点对称的区间上单调性相反
4、如果一个函数既是奇函数有是偶函数,那么有f(x)=0
5、定义域关于原点对称(奇偶函数共有的)
运算法则
(1) 两个偶函数相加或相减所得的和为偶函数。
(2) 两个奇函数相加或相减所得的和为奇函数。
(3) 一个偶函数与一个奇函数相加或相减所得的和为非奇非偶函数。
(4) 两个偶函数相乘或相除所得的积为偶函数。
(5) 两个奇函数相乘或相除所得的积为偶函数。
(6) 一个偶函数与一个奇函数相乘或相除所得的积为奇函数。
(7) 若f(x)为奇函数,且f(x)在x=0时有定义,那么一定有f(0)=0。
(8) 定义在R上的奇函数f(x)必定满足f(0)=0。
(9) 当且仅当f(x)=0(定义域关于原点对称)时,f(x)既是奇函数又是偶函数。
(10) 奇函数在对称区间上的和为零 。
相关推荐

-
菱形的性质与判定,菱形的面积公式是什么
菱形是数学中常见的图形,也是高中数学三维立体空间最常见的构型,虽然菱形本身是非常简单的,但是如果菱形

-
直三棱柱有什么性质?直三棱柱和正三棱柱的区别
初中阶段的我们已经接触到立体图形,但是在高中阶段立体图形的学习更深一步了,其中棱柱的学习的重点,特别

-
双曲线的性质归纳,双曲线的渐近线方程公式
双曲线是高中数学中非常重要的一个知识点,很多学生很容易将双曲线与椭圆的性质弄混淆,其实双曲线与椭圆完
-
反三角函数和三角函数的关系,反三角函数计算公式
在高中阶段数学的学习中,我们已经对于三角函数已经熟记于心了,但是在后面我们还会学到反三角函数,很多人

-
log公式运算法则 log对数函数基本公式
今天小编要给大家介绍的是数学中很重要的知识点log,下面跟着小编来看看log的公式运算法则及基本公式吧! l

-
幂函数的性质,幂函数的运算法则
高中数学中,我们接触到各种各样的函数,其中幂函数是一个重要的函数,可以说学好幂函数是学好高中数学的基