等差数列求和公式怎么求 有哪几种？

　　数学作为理科专业中的一大难点，其复杂的公式和理论是不少学生选择文科的一大推动力，在高中数学的运用中，等差数列求和公式可以说是使用非常频繁的一道公式了，那么等差数列求到底有几种公式，又应该怎么求?有没有什么诀窍呢?看看以下内容吧。

  　　数列求和对按照一定规律排列的数进行求和。求Sn实质上是求{Sn}的通项公式，应注意对其含义的理解。常见的方法有公式法、错位相减法、倒序相加法、分组法、裂项法、数学归纳法、通项化归、并项求和。数列是高中代数的重要内容，又是学习高等数学的基础。在高考和各种数学竞赛中都占有重要的地位。数列求和是数列的重要内容之一，除了等差数列和等比数列有求和公式外，大部分数列的求和都需要有一定的技巧。

    　　【方法一：公式法】

    　　等差数列求和公式:(首项+末项)×项数/2

    　　举例：1+2+3+4+5+6+7+8+9=(1+9)×9/2=45

    　　等比数列求和公式：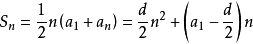

  　　差比数列求和公式：


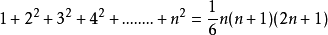  　　其他：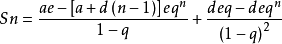


    　　等差数列公式an=a1+(n-1)d

    　　前n项和公式为：Sn=na1+n(n-1)d/2

    　　若公差d=1时：Sn=(a1+an)n/2

    　　若m+n=p+q则：存在am+an=ap+aq

    　　若m+n=2p则：am+an=2ap

    　　以上n均为正整数

    　　文字翻译

    　　第n项的值an=首项+(项数-1)×公差

    　　前n项的和Sn=首项+末项×项数(项数-1)公差/2

    　　公差d=(an-a1)÷(n-1)

    　　项数=(末项-首项)÷公差+1

    　　数列为奇数项时,前n项的和=中间项×项数

    　　数列为偶数项,求首尾项相加,用它的和除以2

    　　等差中项公式2an+1=an+an+2其中{an}是等差数列。